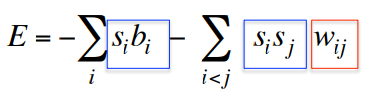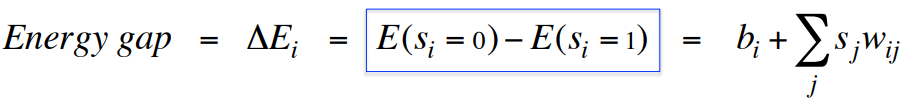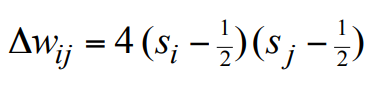Hopfield Nets

  • A Hopfield net is composed of binary threshold units with recurrent connections between them.
  • Recurrent networks of nonlinear units are generally very hard to analyze. They can behave in many different ways:
    • Settle to a stable state
    • Oscillate
    • Follow chaotic trajectories that cannot be predicted far into the future.
  • Hopfield net은 이진 임계 값 단위로 구성되며 반복되는 연결을가집니다.

  • 비선형 단위의 반복적 인 네트워크는 일반적으로 분석하기가 매우 어렵습니다. 그들은 여러 가지 다른 방식으로 행동 할 수 있습니다:

    • 안정된 상태로 정착
    • 진동
    • 예측할 수 없는 혼돈의 궤도를 따라 간다.

  • But John Hopfield (and others) realized that if the connections are symmetric, there is a global energy function.

    • Each binary “configuration” of the whole network has an energy.
      • binary “configuration”=> an assignment of binary values to each neuron in the network.
    • The binary threshold decision rule causes the network to settle to a minimum of this energy function

  • 그러나 John Hopfield (및 다른 사람들)는 연결이 대칭이면 전역 에너지 기능이 있다는 것을 깨달았습니다.

    • 전체 네트워크의 각 바이너리 "구성"에는 에너지가 있습니다.
    • 이진 임계 값 결정 규칙은 네트워크가 이 에너지 기능의 최소치에 도달하게합니다.

The energy function

  • The global energy is the sum of many contributions. Each contribution depends on one connection weight and the binary states of two neurons:

  • This simple quadratic energy function makes it possible for each unit to compute locally how it’s state affects the global energy:

Settling to an energy minimum

  • To find an energy minimum in this net, start from a random state and then update units one at a time in random order.

    • Update each unit to whichever of its two states gives the lowest global energy.
    • i.e. use binary threshold units.

  • 이 네트워크에서 에너지 최소값을 찾으려면 무작위 상태에서 시작하여 유닛을 임의 순서로 한 번에 하나씩 업데이트하십시오.

    • 가장 낮은 global 에너지를 제공하는 두 state 중 어느쪽으로 든 각 유닛을 업데이트하십시오.
    • 바이너리 임계 값 단위를 사용하십시오.

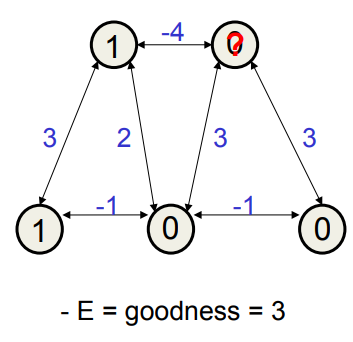
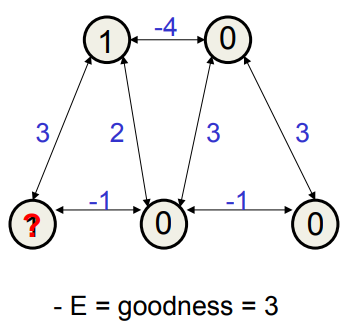
  • A deeper energy minimum

  • The net has two triangles in which the three units mostly support each other.

    • – Each triangle mostly hates the other triangle.

  • The triangle on the left differs from the one on the right by having a weight of 2 where the other one has a weight of 3.

    • – So turning on the units in the triangle on the right gives the deepest minimum.

  • 그물에는 세 개의 유닛이 대부분 서로를 지원하는 두 개의 삼각형이 있습니다.

      • 각 삼각형은 대부분 다른 삼각형을 싫어합니다.

  • 왼쪽에있는 삼각형은 오른쪽에있는 삼각형과 다른 점은 2의 가중치를 가지고 다른 하나는 가중치가 3입니다.

      • 그래서 오른쪽 삼각형의 유닛을 켜면 가장 깊은 최소값을 얻습니다.

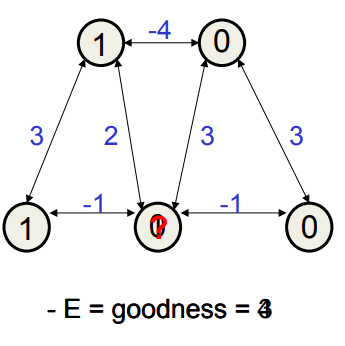
Why do the decisions need to be sequential?

  • If units make simultaneous decisions the energy could go up.
  • With simultaneous parallel updating we can get oscillations.
    • – They always have a period of 2.

  • • If the updates occur in parallel but with random timing, the oscillations are usually destroyed.

  • 단위가 동시에 결정을 내리면 에너지가 상승 할 수 있습니다.

  • 동시 병렬 업데이트로 진동을 얻을 수 있습니다.

      • 항상 2의주기를가집니다.

  • 업데이트가 병렬이지만 임의의 타이밍으로 발생하면 진동이 대개 파괴됩니다.

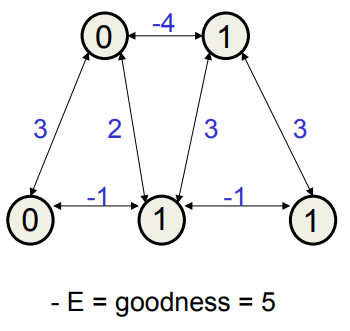
At the next parallel step, both units will turn on. This has very high energy, so then they will both turn off again.

다음 병렬 단계에서 두 장치가 모두 켜집니다. 이것은 매우 높은 에너지를 가지므로 둘 다 다시 꺼질 것입니다.

A neat way to make use of this type of computation(이 계산 유형을 사용하는 깔끔한 방법)

  • • Hopfield (1982) proposed that memories could be energy minima of a neural net.
    • – The binary threshold decision rule can then be used to “clean up” incomplete or corrupted memories.
  • • The idea of memories as energy minima was proposed by I. A. Richards in 1924 in “Principles of Literary Criticism”.

  • • Using energy minima to represent memories gives a content-addressable memory:

    • – An item can be accessed by just knowing part of its content.
      • • This was really amazing in the year 16 BG.
    • – It is robust against hardware damage.
    • – It’s like reconstructing a dinosaur from a few bones

  • Hopfield (1982)는 memories가 신경망의 에너지 최소치 일 수 있다고 제안했다.

      • 이진 임계 값 결정 규칙은 불완전하거나 손상된 메모리를 "정리"하는 데 사용될 수 있습니다.

  • • 에너지 미니마로서의 momory에 대한 생각은 I. Liters에 의해 1924 년 "문학 비평의 원리"에서 제안되었다.

  • • 기억을 표현하기 위해 에너지 최소치를 사용하면 content-addressable 메모리가 생깁니다 :

      • 항목은 내용의 일부만 알면 액세스 할 수 있습니다.
      • • 이것은 16 년 BG에서 정말 놀랍습니다.
      • 하드웨어 손상에 강합니다.
      • 몇 개의 뼈에서 공룡을 재구성하는 것과 같습니다.

Storing memories in a Hopfield net

  • • If we use activities of 1 and -1, we can store a binary state vector by incrementing the weight between any two units by the product of their activities.

  • • 1과 -1의 액티비티를 사용한다면, 액티비티의 곱에 의해 두 단위 사이의 가중치를 증가시킴으로써 바이너리 상태 벡터를 저장할 수 있습니다.

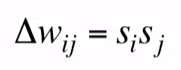
      • This is a very simple rule that is not error-driven. That is both its strength and its weakness

      • 이것은 오류 중심이 아닌 매우 단순한 규칙입니다. 그것은 그것의 힘과 약점이다

    • – We treat biases as weights from a permanently on unit.
    • 바이어스를 영구적 인 단위에서 가중치로 취급합니다.

  • • With states of 0 and 1 the rule is slightly more complicated.

  • 상태가 0과 1이면 규칙이 약간 더 복잡합니다.

results matching ""

    No results matching ""