Lecture 11c Hopfield Nets with hidden units

A different computational role for Hopfield nets

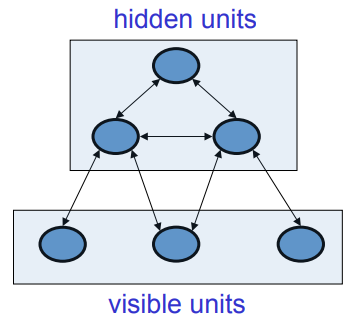
• Instead of using the net to store memories, use it to construct interpretations of sensory input.

– The input is represented by the visible units.

– The interpretation is represented by the states of the hidden units.

– The badness of the interpretation is represented by the energy.

memories을 저장하기 위해 net을 사용하는 대신 sensory input의 해석을 구성하기 위해 그 기억을 사용하십시오.

• 입력은 보이는 단위로 표현됩니다.

• 해석은 숨겨진 유닛의 상태로 표현됩니다.

• 해석의 나쁜 점은 에너지로 표현됩니다.

What can we infer about 3-D edges from 2-D lines in an image?

(이미지의 2-D 라인으로부터 3D 에지를 추론 할 수 있습니까?)

• A 2-D line in an image could have been caused by many different 3-D edges in the world.

• If we assume it’s a straight 3-D edge, the information that has been lost in the image is the 3-D depth of each end of the 2-D line.

– So there is a family of 3-D edges that all correspond to the same 2-D line.

• 이미지에서 2 차원 선은 세계의 여러 3D 입체 가장자리에 의해 발생할 수있었습니다.

• 직선 3D 에지라고 가정하면 이미지에서 손실 된 정보는 2D 라인의 각 끝의 3D 깊이입니다.

• 따라서 같은 3D 라인에 모두 해당하는 3 차원 가장자리의 패밀리가 있습니다.

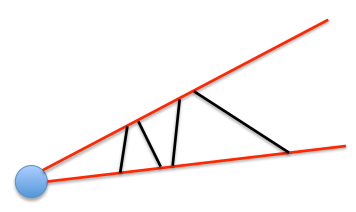
You can only see one of these 3-D edges at a time because they occlude one another.

서로를 가림으로써 한 번에 3 차원 가장자리 중 하나만 볼 수 있습니다.

An example: Interpreting a line drawing

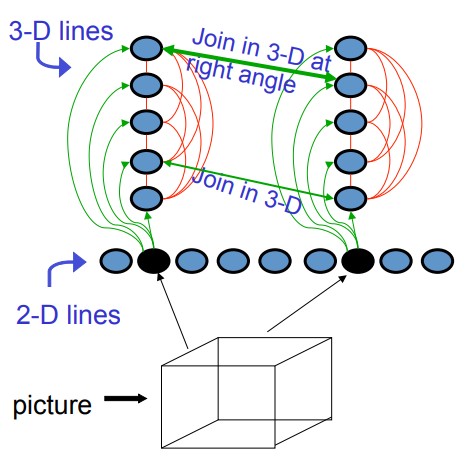
• Use one “2-D line” unit for each possible line in the picture.

– Any particular picture will only activate a very small subset of the line units.

• Use one “3-D line” unit for each possible 3-D line in the scene.

– Each 2-D line unit could be the projection of many possible 3-D lines. Make these 3-D lines compete.

• Make 3-D lines support each other if they join in 3-D.

• Make them strongly support each other if they join at right angles.

• 그림에서 가능한 각 줄마다 하나의 "2D 라인"을 사용하십시오.

• 특정 사진은 라인 단위의 아주 작은 하위 집합 만 활성화합니다.

• 장면에서 가능한 3 차원 선마다 하나의 "3 차원 선"단위를 사용하십시오.

• 각 2-D 라인 유닛은 가능한 많은 3-D 라인의 투영 일 수 있습니다. 이 3-D 라인을 경쟁하게하십시오.

• 3-D 라인이 3-D에 합류하는 경우 서로를 지원합니다.

• 직각으로 결합하면 서로를 강하게지지하게하십시오.

Two difficult computational issues

• • Using the states of the hidden units to represent an interpretation of the input raises two difficult issues:
  • – Search (lecture 11) How do we avoid getting trapped in poor local minima of the energy function?
    • • Poor minima represent suboptimal interpretations.

• – Learning (lecture 12) How do we learn the weights on the connections to the hidden units and between the hidden units?

• • 입력의 해석을 나타내기 위해 숨겨진 유닛의 상태를 사용하면 두 가지 어려운 문제가 발생합니다.

  • • Search (강의 11): 우리는 어떻게 에너지 함수의 poor local minima에 갇히지 않도록해야 합니까?
    • • 불충분 한 미니마는 차선의 해석을 나타냅니다.
• • Learning (강의 12) 숨겨진 유닛과 숨겨진 유닛 간의 연결에 대한 가중치를 어떻게 배울 수 있습니까?