Lecture 11e How a Boltzmann Machine models data

Modeling binary data

(이진 데이터 모델링)

• • Given a training set of binary vectors, fit a model that will assign a probability to every possible binary vector.

  • – This is useful for deciding if other binary vectors come from the same distribution (e.g. documents represented by binary features that represents the occurrence of a particular word).
  • – It can be used for monitoring complex systems to detect unusual behavior.
  • – If we have models of several different distributions it can be used to compute the posterior probability that a particular distribution produced the observed data.

• • 트레이닝 집합의 바이너리 벡터가 주어지면 가능한 모든 바이너리 벡터에 확률을 할당하는 모델을 맞추십시오.

  • • 이것은 다른 바이너리 벡터가 동일한 분포 (예 : 특정 단어의 발생을 나타내는 바이너리 피쳐로 표시되는 문서)에서 왔는지 여부를 결정할 때 유용합니다.
  • • 복잡한 시스템을 모니터링하여 비정상적인 동작을 감지하는 데 사용할 수 있습니다.
  • • 우리가 여러 가지 다른 분포의 모델을 가지고 있다면 그것은 특정 분포가 관측 된 데이터를 생성한 사후 확률을 계산하는 데 사용될 수 있습니다.

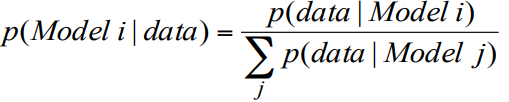
How a causal model generates data

(인과 관계 모델이 데이터를 생성하는 방법)

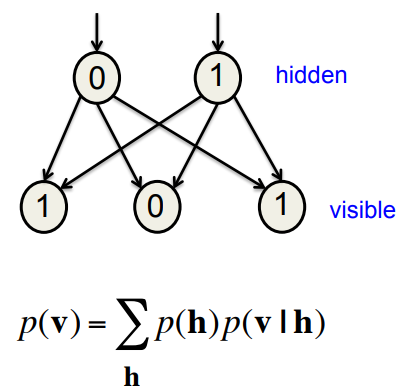
• • In a causal model we generate data in two sequential steps:
  • – First pick the hidden states from their prior distribution.
  • – Then pick the visible states from their conditional distribution given the hidden states.

• • The probability of generating a visible vector, v, is computed by summing over all possible hidden states. Each hidden state is an “explanation” of v.

• • 인과 관계 모델에서 우리는 두 개의 순차적 인 단계로 데이터를 생성합니다 :

  • 먼저 사전분포에서 hidden states를 선택합니다.
  • hidden states의 조건부 분포에서 visible states를 선택합니다.

• • visible vector를 생성할 확률 v는 모든 가능한 visible states를 합산하여 계산됩니다. 각 hidden state는 v에 대한 "설명"입니다.

How a Boltzmann Machine generates data

• • It is not a causal generative model.
• • Instead, everything is defined in terms of the energies of joint configurations of the visible and hidden units.
• • The energies of joint configurations are related to their probabilities in two ways.
  • – We can simply define the probability to be
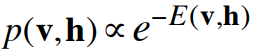
  • – Alternatively, we can define the probability to be the probability of finding the network in that joint configuration after we have updated all of the stochastic binary units many times.

• • These two definitions agree.

• • 인과 관계 생성 모델이 아닙니다.

• • 대신 모든 것은 visible units와 hidden units의 joint configurations 에너지로 정의됩니다.

• • 연결 구성의 에너지는 두 가지 방법으로 확률과 관련됩니다.

  • • 우리는 단순히 확률을 정의 할 수 있습니다.
  • • 또는 확률적 이진 단위를 여러 번 업데이트 한 후에 해당 공동 구성에서 네트워크를 찾을 확률이 될 확률을 정의 할 수 있습니다.

• •이 두 정의가 일치합니다.

Using energies to define probabilities

• The probability of a joint configuration over both visible and hidden units depends on the energy of that joint configuration compared with the energy of all other joint configurations.
• visible units 과 hidden units 모두에 대한 The probability of a joint configuration 은 다른 모든 joint configuration 의 에너지와 비교한 joint configuration 의 에너지에 따라 달라집니다.

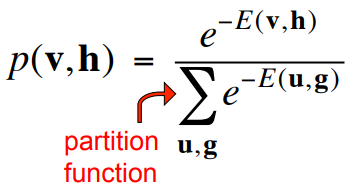
• The probability of a configuration of the visible units is the sum of the probabilities of all the joint configurations that contain it.
• The probability of a configuration of the visible units 은 그것을 포함하고 있는 모든 joint configurations 의 확률의 합입니다.

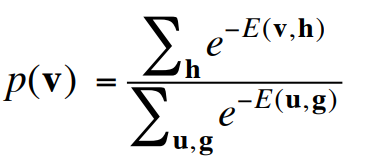
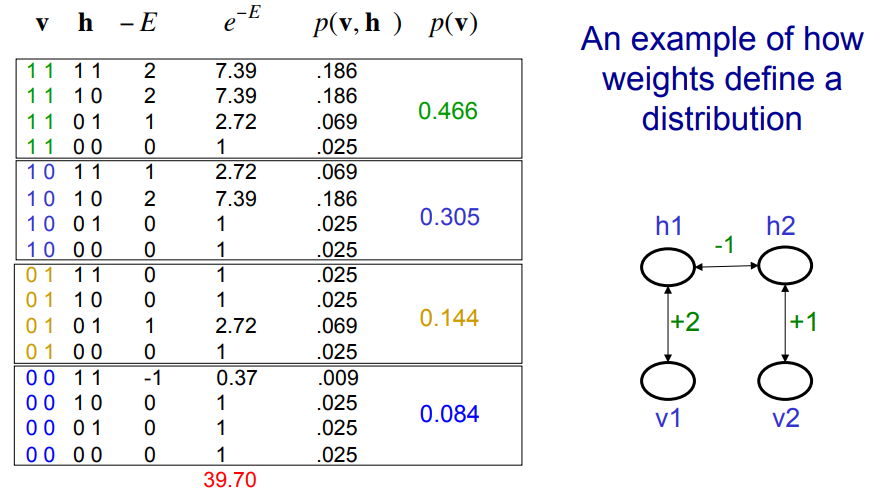바이어스는 0으로 가정하고, 11a 강의 자료의 식 참조

Getting a sample from the model

(모델에서 샘플 가져 오기)

• • If there are more than a few hidden units, we cannot compute the normalizing term (the partition function) because it has exponentially many terms.
• • So we use Markov Chain Monte Carlo to get samples from the model starting from a random global configuration:
  • – Keep picking units at random and allowing them to stochastically update their states based on their energy gaps.

• • Run the Markov chain until it reaches its stationary distribution (thermal equilibrium at a temperature of 1).

  • – The probability of a global configuration is then related to its energy by the Boltzmann distribution.

• • hidden units이 몇 개 이상일 경우 기하 급수적으로 많은 term 가 있기 때문에 정규화 term (파티션 함수)를 계산할 수 없습니다.

• • Markov Chain Monte Carlo를 사용하여 임의의 전역 구성에서 시작하여 모델에서 샘플을 가져옵니다.

  • • 유닛을 무작위로 선택하고 에너지 갭을 기반으로 상태를 확률 적으로 업데이트 할 수있게하십시오.

• • 마르코프 체인이 정상 분포 (온도 1에서의 열 평형)에 도달 할 때까지 실행하십시오.

  • • 글로벌 구성의 확률은 볼츠만 분포에 의해 에너지와 관련이있다.
• 

Getting a sample from the posterior distribution over hidden configurations for a given data vector

(주어진 데이터 벡터에 대한 숨겨진 구성에 대한 사후 분포에서 샘플 얻기)

• • The number of possible hidden configurations is exponential so we need MCMC to sample from the posterior.
  • – It is just the same as getting a sample from the model, except that we keep the visible units clamped to the given data vector.
    • • Only the hidden units are allowed to change states

• • Samples from the posterior are required for learning the weights. Each hidden configuration is an “explanation” of an observed visible configuration. Better explanations have lower energy.

• 가능한 hidden configurations의 수는 기하급수적이므로 우리는 posterior로부터 샘플링하기 위해 MCMC가 필요합니다.

  • • visible units를 주어진 데이터 벡터에 고정시키는 것을 제외하고는 모델에서 샘플을 얻는 것과 같습니다.
    • hidden units 만 상태를 변경할 수 있습니다

• 가중치를 배우기 위해서는 posterior의 샘플이 필요합니다. 각 hidden configuration은 관찰된 visible configuration의 "설명"입니다. 더 나은 설명은 에너지가 낮습니다.