Word Embedding 관련 학습들은 기본적으로 언어학의 ‘
‘ 라는 가정에 입각하여 이루어진다. 이는, ‘비슷한 분포를 가진 단어들은 비슷한 의미를 가진다’ 라는 의미이다.
가장 먼저 등장한 아키텍쳐는 Feed-Forward Neural Net Language Model (NNLM) 이라는 모델이다.
– NNLM(Feed-Forward Neural Net Language Model)
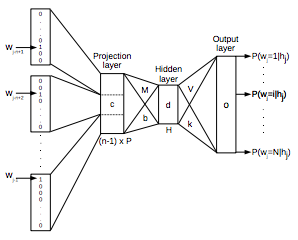
NNLM Structure
- Input Layer
- Projection Layer
- Hidden Layer
- Output Layer
순서
- 일단, 현재 보고 있는 단어 이전의 단어들 N개를 one-hot encoding 으로 벡터화한다.
- 사전의 크기를 V라고 하고 Projection Layer의 크기를 P라고 했을 때, 각각의 벡터들은 VxP 크기의 Projection Matrix에 의해 다음 레이어로 넘어가게 된다.
- 그 다음부터는 우리가 알고 있는 기본적인 MLP 구조와 매우 유사하다.
- Projection Layer의 값을 인풋이라고 생각하고, 크기 H짜리 hidden layer를 거쳐서 output layer에서 ‘각 단어들이 나올 확률’을 계산한다.
- 이를 실제 단어의 one-hot encoding 벡터와 비교하서 에러를 계산하고, 이를 back-propagation 해서 네트워크의 weight들을 최적화해나가는 것이 기본적인 구조이다.
- 이 네트워크에서 최종적으로 사용하게 될 단어의 벡터들은 Projection Layer의 값들로서, 각 단어들은 크기 P의 벡터가 된다.
단점
- 몇 개의 단어를 볼 건지에 대한 파라미터 N이 고정되어 있고, 정해주어야 한다.
- 이전의 단어들에 대해서만 신경쓸 수 있고, 현재 보고 있는 단어 앞에 있는 단어들을 고려하지 못한다.
- 가장 치명적인 단점으로, 느리다.
– RNNLM(Recurrent Neural Network Language Modeling )

RNNLM Structure
RNNLM은 기본적으로 NNLM을 Recurrent Neural Network의 형태로 변형한 것이다.
이 네트워크는 기본적으로 Projection Layer 없이 Input, Hidden, Output Layer로만 구성되는 대신, Hidden Layer에 Recurrent한 연결이 있어 이전 시간의 Hidden Layer의 입력이 다시 입력되는 형식으로 구성되어 있다. 이 네트워크의 경우 그림에서 U라고 나타나 있는 부분이 Word Embedding으로 사용이 되며, Hidden Layer의 크기를 H라고 할 때 각 단어는 길이 H의 벡터로 표현될 것이다.
RNNLM의 경우 NNLM과는 달리 몇 개의 단어인지에 대해 정해줄 필요가 없이, 단순하게 학습시켜줄 글의 단어를 순차적으로 입력해주는 방식으로 학습을 진행하면 된다. 학습을 진행하면서 Recurrent한 부분이 일종의 Short-Term 메모리 역할을 하면서 이전 단어들을 보는 효과를 낼 것이다. 또한, RNNLM은 NNLM보다 연산량이 적기도 하다. 이 모델이 한 단어를 처리하는 데에 필요로 하는 연산량을 생각해보면
- Input Layer에서 Hidden Layer로 넘어가는 데에 H
- hidden(t-1)에서 hidden(t)로 넘어가는 벡터를 계산하는 데에 HxH
- Hidden Layer에서 Output 결과를 내기 위해 모든 단어에 대해 확률계산을 해야하므로 HxV
로, H를 무시하면 O(HxH + HxV) 이다. 일반적인 경우라면 HxV가 Dominating Term이 되겠지만, 앞서 말했듯이 이는 Hx lnV로 줄일 수 있는 테크닉이 존재한다. 따라서 이 모델은 한 단어를 진행하는 데에 O(HxH)의 계산량을 필요로 한다. H를 아까와 같이 500으로 잡는다면 O(25만)의 연산량이다. RNNLM에 비해 대략 1/N배로 줄어들어 계산이 빨라졌다.
NNLM과 RNNLM 모두 단어 벡터화 학습을 하기에 좋은 방법이다. 그러나 문제는 자연어 처리 분야의 특성상 굉장히 많은 데이타를 넣어서 학습시켜줘야 각 단어에 대한 정확한 표현법을 학습할 수 있을 것이라는 것이다. 따라서 성능도 성능이지만 학습을 빠르게 할 수 있는 방법이 필요하게 되었고, 이 문제를 해결하며 이 분야의 state-of-the-art로 떠오른 방법이 바로 word2vec이다.
# Word2Vec
word2vec은 2013년 구글에서 발표된 연구로, Tomas Mikolov라는 사람을 필두로 여러 연구자들이 모여서 만든 Continuous Word Embedding 학습 모형이다. 재밌는 점은, 이 논문을 집필한 사람 중 Jeffery Dean (구글의 전설적인 프로그래머로 MapReduce등을 만듬) 도 있다는 점이다. 이 모델이 기존 Neural Net 기반 학습방법에 비해 크게 달라진 것은 아니지만, 계산량을 엄청나게 줄여서 기존의 방법에 비해 몇 배 이상 빠른 학습을 가능케 하여 현재 가장 많은 이들이 사용하는 Word Embedding 모델이 되었다.
기존 연구들과 달리, 이 연구에서는 학습을 시키기 위한 네트워크 모델을 두 가지 제시하였다. 한 가지는 CBOW(Continuous Bag-of-Words) 모델이고, 다른 하나는 Skip-gram 모델이다.
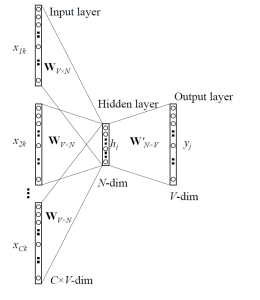
CBOW Architecture
CBOW 모델의 경우 다음과 같은 방식을 채용하고 있하고 생각할 수 있을 것 같다. “집 앞 편의점에서 아이스크림을 사 먹었는데, ___ 시려서 너무 먹기가 힘들었다.” 라는 문장에서, 사람들은 ___ 부분에 들어갈 단어가 정확하게 주어지지 않아도 앞 뒤의 단어들을 통해 ‘이가’ 라는 말이 들어갈 것을 추측할 수 있다. CBOW 모델도 마찬가지의 방법을 사용한다. 주어진 단어에 대해 앞 뒤로 C/2개 씩 총 C개의 단어를 Input으로 사용하여, 주어진 단어를 맞추기 위한 네트워크를 만든다.
CBOW 모델은 크게 Input Layer, Projection Layer, Output Layer로 이루어져 있다. 그림에는 중간 레이어가 Hidden Layer라고 표시되어 있기는 하지만, Input에서 중간 레이어로 가는 과정이 weight를 곱해주는 것이라기 보다는 단순히 Projection하는 과정에 가까우므로 Projection Layer라는 이름이 더 적절할 것 같다. Input Layer에서 Projection Layer로 갈 때는 모든 단어들이 공통적으로 사용하는 VxN 크기의 Projection Matrix W가 있고 (N은 Projection Layer의 길이 = 사용할 벡터의 길이), Projection Layer에서 Output Layer로 갈 때는 NxV 크기의 Weight Matrix W’ 가 있다. (주의해야할 점은, 두 행렬은 별개의 행렬이라는 점이다. 예전 What’s Cooking 대회를 할 때는 이 W’ 가 W의 transpose라고 생각하고 구현했었다. 당시에 어떻게든 봐줄만한 결과가 나왔던 것이 신기하다..) Input에서는 NNLM 모델과 똑같이 단어를 one-hot encoding으로 넣어주고, 여러 개의 단어를 각각 projection 시킨 후 그 벡터들의 평균을 구해서 Projection Layer에 보낸다. 그 뒤는 여기에 Weight Matrix를 곱해서 Output Layer로 보내고 softmax 계산을 한 후, 이 결과를 진짜 단어의 one-hot encoding과 비교하여 에러를 계산한다.
CBOW 모델에서 하나의 단어를 처리하는 데에 드는 계산량은 다음과 같다.
- C개의 단어를 Projection 하는 데에 C x N
- Projection Layer에서 Output Layer로 가는 데에 N x V
따라서 전체 계산량은 CxN + NxV가 되는데, 앞서 말한 V를 ln V로 줄이는 테크닉을 사용하면 전체 계산량이 CxN + N x lnV가 된다. 이 식을 잘 보면, 이 모델이 앞서 다른 모델들에 비해 왜 계산이 빠른지 알 수 있다. CBOW 모델에서 보통 C는 10 내외의 크기로 잡으므로, 전체 계산량은 결국 Projection Layer의 크기 N과 log-사전크기의 lnV의 크기의 곱에 비례하게 된다. 즉, C=10, N=500, V=1,000,000으로 잡아도 500 x (10+ln(1,000,000)) = 약 10000의 계산량밖에 들지 않는 것이다. 이는 앞서 확인한 NNLM이나 RNNLM에 비해 정말 엄청나게 줄어든 계산량이라는 것을 확인할 수 있다.

Skip-gram Architecture
다른 하나의 모델인 Skip-gram 모델은 CBOW와는 반대 방향의 모델이라고 생각할 수 있을 것 같다. 현재 주어진 단어 하나를 가지고 주위에 등장하는 나머지 몇 가지의 단어들의 등장 여부를 유추하는 것이다. 이 때 예측하는 단어들의 경우 현재 단어 주위에서 샘플링하는데, ‘가까이 위치해있는 단어일 수록 현재 단어와 관련이 더 많은 단어일 것이다’ 라는 생각을 적용하기 위해 멀리 떨어져있는 단어일수록 낮은 확률로 택하는 방법을 사용한다. 나머지 구조는 CBOW와 방향만 반대일 뿐 굉장히 유사하다.
Skip-gram 모델에서 하나의 단어를 처리하는 데에 드는 계산량은 다음과 같다. C개의 단어를 샘플링했다고 할 때,
- 현재 단어를 Projection 하는 데에 N
- Output을 계산하는 데에 N x V, 테크닉을 사용하면 N x ln V
- 총 C개의 단어에 대해 진행해야 하므로 총 C배
로 총 C(N + N x lnV) 만큼의 연산이 필요하다. 즉 이 모델도 CBOW 모델같이 N x lnV에 비례하는 계산량을 가진 모델이기는 하지만, 몇 개의 단어를 샘플링하냐에 따라서 계산량이 그것에 비례하여 올라가게 되므로 CBOW 모델에 비해서는 학습이 느릴것이다.
CBOW 모델과 Skip-gram 모델을 비교하면 CBOW의 모델이 조금 더 논리적이라고 개인적으로 생각하지만, 실제 실험 결과에서는 Skip-gram이 CBOW에 비해 전체적으로 다소 좋은 결과를 내는 추세를 보인다. 현재는 대부분의 사람들이 Skip-gram 모델을 사용하는 것 같다.
# V to ln(V) : Complexity Reduction
앞서 말한 기본적인 CBOW와 Skip-gram 모델을 그대로 구현해서 돌릴 경우 생각보다 학습이 오래 걸리는 것을 확인할 수 있을 것이다. 이는 앞서 말한 V에 관련된 항 때문이다. 영어 단어의 총 개수는 백만개가 넘는다고 한다. 그런데 네트워크의 Output Layer에서 Softmax 계산을 하기 위해서는 각 단어에 대해 전부 계산을 해서 normalization을 해주어야 하고, 이에 따라 추가적인 연산이 엄청나게 늘어나서 대부분의 연산을 이 부분에 쏟아야 한다. 이를 방지하기 위해서 이 부분의 계산량을 줄이는 방법들이 개발되었는데, Hierarchical Softmax와 Negative Sampling이 그 방법들이다.
– Hierarchical Softmax
Hierarchical Softmax는 계산량이 많은 Softmax function 대신 보다 빠르게 계산가능한 multinomial distribution function을 사용하는 테크닉이다. 이 방법에서는 각 단어들을 leaves로 가지는 binary tree를 하나 만들어놓은 다음(complete 할 필요는 없지만, full 할 필요는 있을 것 같다), 해당하는 단어의 확률을 계산할 때 root에서부터 해당 leaf로 가는 path에 따라서 확률을 곱해나가는 식으로 해당 단어가 나올 최종적인 확률을 계산한다.

Example Binary Tree for Hierarchical Softmax

Probability Equation for Hierarchical Softmax
설명하기 전 이 방법에서 사용하는 notation들을 살펴보자.
- L(w)는 w라는 leaf에 도달하기 까지의 path의 길이를 의미한다.
- n(w, i) 는 root에서부터 w라는 leaf에 도달하는 path에서 만나는 i번째 노드를 의미한다. n(w, 1)은 루트가 될 것이고, n(w, L(w)) 는 w가 될 것이다.
- ch(node) 는 node의 고정된 임의의 한 자식을 의미하며, 여기서는 단순하게 node의 왼쪽 자식이라고 생각하겠다. 이렇게 생각해도 무방하다.
- [[x]] 는 x가 true일 경우 1, false일 경우 -1을 반환하는 함수로 정의한다.
- Hierarchial Softmax를 사용할 경우 기존 CBOW나 Skip-gram에 있던 W’ matrix를 사용하지 않게 된다. 대신, V-1개의 internal node가 각각 길이 N짜리 weight vector를 가지게 된다. 이를 v’_i 라고 하고 학습에서 update 해준다.
- h는 hidden layer의 값 벡터이다.
- sigma(x)는 sigmoid function 1/(1+exp(-x)) 이다.
이렇게 정의하고 위의 식과 같은 방법으로 p(w)를 계산한다고 해보자. 이 경우 각 스텝마다 길이 N짜리 벡터 두 개의 내적이 일어나므로 계산량 N이 필요하며, binary tree를 잘 만들었을 경우 평균적으로 루트로부터 leaf까지의 거리는 평균 O(lnV)일 것이므로 총 N x lnV의 계산량만으로 특정 단어가 나올 확률을 계산할 수 있다. 네트워크의 Error Function을 Categorical Cross-entropy 로 사용할 경우 최종 Error를 계산하기 위해서 해당하는 단어에 대해서만 확률을 계산하면 되므로, 다른 추가적인 연산 없이 O(N x lnV)의 계산량만으로 계산이 끝난다.
또한 특정 hidden layer 값에 대해 모든 단어들의 확률을 더한 sigma p(w_i | hidden layer) 를 생각해보자. Full binary tree를 산정하고 v_node와 h의 내적 값을 x라고 생각할 경우,
- 특정 node에서 왼쪽 자식으로 갈 때의 확률 = sigmoid(x)
- 특정 node에서 오른쪽 자식으로 갈 때의 확률 = sigmoid(-x) = 1-sigmoid(x)
따라서 특정 노드에서 왼쪽, 오른쪽 자식으로 갈 확률을 더하면 1이 된다. 이를 이용하면, sigma p(w_i | hidden layer) 값이 1이라는 것을 쉽게 보일 수 있을 것이다. Softmax function의 계산이 오래 걸렸던 것은 확률 계산을 위해 모든 결과에 대한 합을 1로 만들어주기 위함이었다. 이 과정에서 최종적으로 나온 output값에 대해 일일히 계산을 해주어서 전체 합으로 normalize를 해주었기 때문에 V 만큼의 계산이 더 필요했던 것인데, 이 Hierarchical Softmax를 사용하면 전체 확률에 대한 계산 없이 전체 합을 1로 만들어 줄 수 있어 좋은 multinomial distribution function으로 사용할 수 있게 되는 것이다.
word2vec 논문에서는 이러한 Binary Tree로 Binary Huffman Tree를 사용했다고 한다. Huffman Tree를 사용할 경우 자주 등장하는 단어들은 보다 짧은 path로 도달할 수 있기 때문에 전체적인 계산량이 더 낮아지는 효과를 볼 수 있을 것이다. 또한 Huffman Tree는 Full Binary Tree이기 때문에 Hierarchical Softmax의 조건에도 부합한다.
– Negative Sampling
Negative Sampling은 Hierarchial Softmax의 대체재로 사용할 수 있는 방법이다. 전체적인 아이디어는 ‘Softmax에서 너무 많은 단어들에 대해 계산을 해야하니, 여기서 몇 개만 샘플링해서 계산하면 안될까?’ 라는 생각에서 시작된다. 전체 단어들에 대해 계산을 하는 대신, 그 중에서 일부만 뽑아서 softmax 계산을 하고 normalization을 해주는 것이다. 즉, 계산량은 N x V에서 N x K (K = 뽑는 샘플의 갯수)로 줄어들 것이다. 이 때 실제 target으로 사용하는 단어의 경우 반드시 계산을 해야하므로 이를 ‘positive sample’ 이라고 부르고, 나머지 ‘negative sample’ 들을 어떻게 뽑느냐가 문제가 된다. 이 뽑는 방법을 어떻게 결정하느냐에 따라 Negative sampling의 성능도 달라지고, 이는 보통 실험적으로 결정한다.
그런데 word2vec의 경우 기존과는 다른 새로운 Error Function을 정의해서 사용한다. 그들은

다음과 같은 목표를 maximize 하도록 weight을 조정한다. 이 때 좌측 항은 positive sample에 대한 항이고, 우측은 뽑은 negative sample들에 대한 항이다. 왜 이러한 objective function을 사용하게 되었는지는 논문 [5]에 자세하게 설명되어 있다. 기본적으로 보고있는 단어 w와 목표로 하는 단어 c를 뽑아서 (w,c)로 둔 후, positive sample의 경우 ‘이 (w,c) 조합이 이 corpus에 있을 확률’ 을 정의하고, negative sample의 경우 ‘이 (w,c) 조합이 이 corpus에 없을 확률’을 정의하여 각각을 더하고 log를 취해서 정리하면 위과 같은 형태의 식이 나온다. 자세한 수리적 전개 과정을 보고싶은 분들은 논문 [5]를 참조하시면 되겠다.
보통 Negative Sampling에서 샘플들을 뽑는 것은 ‘Noise Distribution’ 을 정의하고 그 분포를 이용하여 단어들을 일정 갯수 뽑아서 사용하는데, 논문에서는 여러 분포를 실험적으로 사용해본 결과 ‘Unigram Distribution의 3/4 승’ (여기서 Unigram Distribution은 단어가 등장하는 비율에 비례하게 확률을 설정하는 분포라고 할 수 있다. 이 경우 각 확률을 3/4승 해준 후, Normalization factor로 나누어서 단어가 등장할 확률로 사용한 것이다) 을 이용한 분포를 이용해서 실험한 결과 unigram, uniform 등 다른 분포들보다 훨씬 좋은 결과를 얻을 수 있었다고 한다.
– Further Method : Subsampling Frequent Words
Hierarchical Softmax와 Negative Sampling은 모델 자체의 계산복잡도를 줄이기 위한 테크닉이었다. 여기서 추가적인 방법으로, 논문에서는 ‘the’, ‘a’, ‘in’ 등 자주 등장하는 단어들을 확률적으로 제외하여 학습 속도를 향상시켰을 뿐만 아니라 성능까지 향상시켰다. 단어 w의 등장 빈도를 f(w)라고 할 때, 학습할 때 각 단어는

의 확률로 제외된다. 이 때 t는 빈도가 일정값 이상일 때만 제외하겠다는 느낌의 threshold 값인데, 논문에서는 10^-5 의 값을 사용했을 때 가장 좋은 결과를 얻을 수 있었다고 한다.
# Performance Comparison
이 파트는 여러 단어의 벡터화 학습법에 대한 실험적인 성능 비교를 다루는 부분이다. 이 때 성능을 측정하기 위해 사용한 실험은 ‘Analogy Reasoning Task’ 이다.

Example Word Pairs for Analogy Reasoning Task
Analogy Reasoning Task는 어떤 단어의 Pair, 예를 들어 (Athens, Greece) 라는 Pair가 주어졌을 때, 다른 단어 Oslo를 주면 이 관계에 상응하는 다른 단어를 제시하는 방식의 시험이다. 이러한 ‘관계’ 에는 수도, 화폐, 주와 도시 등 내용에 관련된 ‘semantic’ 한 관계가 5개 있으며, 문법에 관련된 ‘syntactic’ 한 관계가 9개 있다.
만약 지금까지 설명한 방법들로 각 단어의 벡터를 잘 학습했다고 할 경우 이 문제의 답을 추론하는 것은 간단할 것이다. 예를 들면, vector(Greece) – vector(Athens) + vector(Oslo)를 하고 이 벡터에 가장 가까운 벡터를 찾으면 Norway가 나올 것이라고 기대할 수 있을 것이다.
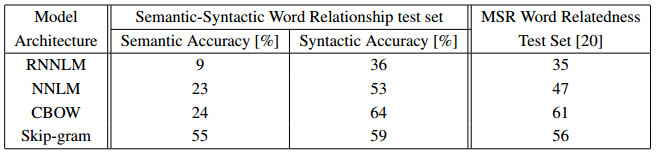
Analogy Reasoning Task Results for Various Models. Word Dimension = 640
위는 단어 벡터 길이를 640으로 하고 다양한 모델을 이용하여 학습시켰을 때의 결과이다. 보다시피 RNNLM과 NNLM에 비해 CBOW와 Skip-gram이 Semantic, Syntactic 문제에 대해 훨씬 더 좋은 결과를 내는 것을 알 수 있다. 또한 두 모델을 비교해보면 Skip-gram이 Syntactic 문제의 정확도는 조금 떨어지기는 하지만, Semantic 문제에 대해서는 훨씬 높은 정확도를 보였다.

Analogy Reasoning Task Results for Various Methods. Word Dimension = 300
위 표는 모델을 300차원 Skip-gram으로 고정한 후 실험한 결과이다. NEG-k는 k개 단어를 선택한 negative sampling이고, HS-Huffman은 Huffman Tree를 이용한 Hierarchical Softmax이다. (NCE-k는 negative sampling과 유사한 방법으로, Noise Contrastive Estimation이라고 하는 방법이다. 논문에서는 이 방법을 기초로 하여 목적 함수를 조금 바꾸어서 Negative Sampling을 만든 것이다.) 실험 결과 전체적으로 Hierarchical Softmax를 사용한 것 보다 Negative Sampling을 사용했을 때 더 결과가 좋은 것을 발견할 수 있다. 또한, 자주 등장하는 단어를 subsampling 했을 때 학습 시간이 눈에 띄게 줄어든 것 뿐만 아니라 성능까지 어느정도 향상되었다.
단, 이 표에서 Hierarchical Softmax의 성능이 낮았다고 실제 이 방법이 나쁜 방법인 것은 아니다. 이 실험 말고도 Phrase에 대해 비슷한 Task를 만들어서 실험을 진행하였는데, 이 경우 HS가 NS보다 훨씬 좋은 성능을 보였다. 즉 어떤 문제에 적용하는 지에 따라 성능이 달라지는 것으로 사료된다.
# Closing
word2vec 은 기존 단어 벡터 학습에 비해 훨씬 빠른 시간에 학습을 하면서도 더 좋은 성능을 낼 수 있게 하여 NLP 분야의 새로운 지평을 열었다. 이렇게 각 단어별 벡터를 잘 학습할 수 있다면 이러한 벡터들을 가지고 할 수 있는 일은 무궁무진하게 넓어진다. 단 단어별 벡터를 안다고 이를 단순하게 문장이나 문단의 의미로 확장시킬 수 있는 것은 아니다. 이를 위해서 각 문장이나 문단의 의미까지 파악하기 위해 문장이나 문단을 벡터로 변환하는 sentence2vec, paragraph2vec 등의 연구가 계속 이어지고 있다. 이 word2vec 코드는 이미오픈소스화되어 공개되어 있다. 학습 모델 및 이미 학습되어 있는 결과들, 그리고 여러 실험을 해볼 수 있는 도구이다. python에는gensim이라는 라이브러리가 있는데, 이 라이브러리의 기능중 하나로 word2vec을 사용할 수도 있다. 이 라이브러리는 C로 최적화가 이루어져 있어 단순히 NumPy로 구현하는 것 보다 70배의 속도를 낸다고 한다. 실제로 word2vec을 다뤄보고싶으신 분들은 위의 툴들을 참고하시길 바란다.
# References
[1] T. Mikolov, et al., Efficient Estimation of Word Representations in Vector Space.[arXiv]
[2] T. Mikolov, et al., Distributed Representations of Words and Phrases.[Link]
[3] X. Rong, word2vec Parameter Learning Explained.[Link]
[4] J. Garten, et al., Combining Distributed Vector Representations for Words.[Link]
[5] Y. Goldberg, et al., word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method.[arXiv]