Lecture 12b More efficient ways to get the statistics

A better way of collecting the statistics

• • If we start from a random state, it may take a long time to reach thermal equilibrium.
  • – Also, its very hard to tell when we get there.
• • Why not start from whatever state you ended up in last time you saw that datavector?
  • – This stored state is called a “particle”.
• • Using particles that persist to get a “warm start” has a big advantage:
  • – If we were at equilibrium last time and we only changed the weights a little, we should only need a few updates to get back to equilibrium.
• •무작위 상태에서 시작하면 열 평형에 도달하는 데 오랜 시간이 걸릴 수 있습니다.
  • 또한 우리가 거기에 도착했을 때 알기가 매우 어렵습니다.
• • 지난 번에 그 상태를 보았던 어떤 상태에서 시작해서 왜 그 데이터 벡터를 보지 못했습니까?
  • -이 저장된 상태를 "입자"라고합니다.
• • "웜 스타트"를 지속하는 입자를 사용하면 큰 장점이 있습니다.
  • 지난 시간에 평형 상태에 있었고 우리가 가중치를 조금만 변경했다면 평형 상태로 돌아 가기 위해 몇 가지 업데이트가 필요했습니다.

Neal’s method for collecting the statistics (Neal 1992)

• Positive phase: Keep a set of “data-specific particles”, one per training case. Each particle has a current value that is a configuration of the hidden units.
  • – Sequentially update all the hidden units a few times in each particle with the relevant datavector clamped.
  • – For every connected pair of units, average Si, Sj over all the data-specific particles.
• Negative phase: Keep a set of “fantasy particles”. Each particle has a value that is a global configuration.
• – Sequentially update all the units in each fantasy particle a few times.
• – For every connected pair of units, average Si, Sj over all the fantasy particles.
• • Positive phase : 교육 사례 별로 하나 씩 "데이터 특정 입자"세트를 유지합니다. 각 파티클은 숨겨진 유닛의 구성 인 현재 값을 가집니다.
  • • 각 입자에서 모든 숨겨진 유닛을 순차적으로 업데이트하고 관련 데이터 벡터를 클램프합니다.
  • • 연결된 모든 단위 쌍에 대해 모든 데이터 특정 입자에 대해 평균 Si, Sj를 구합니다.
• 부정적인 단계 : 일련의 "판타지 입자"를 유지하십시오. 각 입자에는 전역 구성 값이 있습니다.
  • • 각 판타지 입자의 모든 유닛을 순차적으로 몇 번 업데이트하십시오.
  • • 모든 연결된 단위 쌍에 대해 모든 환상 입자에 대해 Si, Sj를 평균합니다.

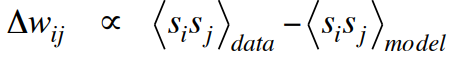
Adapting Neal’s approach to handle mini-batches

(미니 배치 처리를위한 Neal의 접근 방식 수정
)

• • Neal’s approach does not work well with mini-batches.
  • – By the time we get back to the same datavector again, the weights will have been updated many times.
  • – But the data-specific particle will not have been updated so it may be far from equilibrium.
• • A strong assumption about how we understand the world:
  • – When a datavector is clamped, we will assume that the set of good explanations (i.e. hidden unit states) is uni-modal.
  • – i.e. we restrict ourselves to learning models in which one sensory input vector does not have multiple very different explanations.
• • Neal의 접근 방식은 미니 일괄 처리에서는 잘 작동하지 않습니다.
  • • 동일한 데이터 벡터로 다시 돌아갈 때까지 가중치가 여러 번 업데이트됩니다.
  • • 그러나 데이터 특정 입자는 업데이트되지 않았으므로 평형에서 멀어 질 수 있습니다.
• • 우리가 세상을 어떻게 이해하는지에 대한 강한 가정 :
  • • 데이터 벡터가 클램핑 될 때, 우리는 좋은 설명 (즉, 은닉 단위 상태)의 세트가 단일 모달이라고 가정 할 것이다.
  • 즉, 하나의 감각 입력 벡터가 여러 가지 매우 다른 설명을 가지지 않는 학습 모델로 제한한다.

The simple mean field approximation

• • If we want to get the statistics right, we need to update the units stochastically and sequentially.
• • But if we are in a hurry we can use probabilities instead of binary states and update the units in parallel.
• • To avoid biphasic oscillations we can use damped mean field.
• • 통계를 올바르게 얻으려면 단위를 확률적으로 순차적으로 업데이트 해야합니다.
• • 그러나 우리가 서두르면 이진 상태 대신 확률을 사용하고 단위를 병렬로 업데이트 할 수 있습니다.
• • 2 상 진동을 피하기 위해 감쇠 평균 필드를 사용할 수 있습니다.
• 

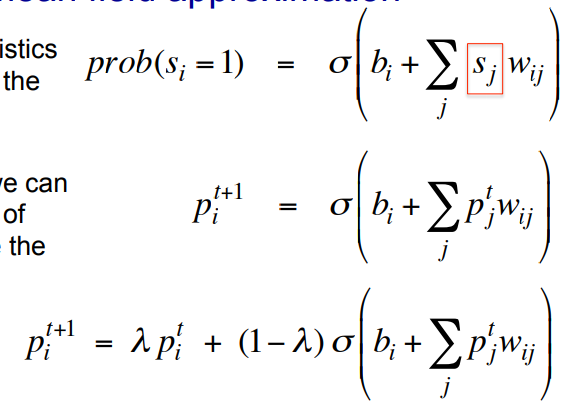
An efficient mini-batch learning procedure for Boltzmann Machines (Salakhutdinov & Hinton 2012)

• • Positive phase: Initialize all the hidden probabilities at 0.5.
• – Clamp a datavector on the visible units.
• – Update all the hidden units in parallel until convergence using mean field updates.
• – After the net has converged, record Pi, Pj for every connected pair of units and average this over all data in the mini-batch.
• • Negative phase: Keep a set of “fantasy particles”. Each particle has a value that is a global configuration.
• – Sequentially update all the units in each fantasy particle a few times.

• – For every connected pair of units, average Si, Sj over all the fantasy particles.

• •Positive phase : 모든 숨겨진 확률을 0.5로 초기화합니다.

• • visible units로 데이터 벡터를 클램프합니다.
• • 평균 필드 업데이트를 사용하여 수렴 할 때까지 모든 hidden units을 병렬로 업데이트하십시오.
• • net 이 수렴 한 후에는 연결된 단위 쌍마다 Pi, Pj를 기록하고 미니 배치의 모든 데이터에 대해 평균을 구합니다.
• • Negative phase : 일련의 "fantasy particles"를 유지하십시오. 각 입자에는 global configuration 값이 있습니다.
• • 각 antasy particles의 모든 유닛을 순차적으로 몇 번 업데이트하십시오.
• • 모든 연결된 단위 쌍에 대해 모든 환상 입자에 대해 Si, Sj를 평균합니다.

Making the updates more parallel

• • In a general Boltzmann machine, the stochastic updates of units need to be sequential.
• • There is a special architecture that allows alternating parallel updates which are much more efficient:
  • – No connections within a layer.
  • – No skip-layer connections.
• • This is called a Deep Boltzmann Machine (DBM)
  • – It’s a general Boltzmann machine with a lot of missing connections.
• • 일반적인 볼츠만 기계에서 단위의 확률적 업데이트는 순차적이어야합니다.
• • 훨씬 효율적인 병렬 업데이트를 번갈아 수행 할 수 있는 특별한 아키텍처가 있습니다.
  • • 레이어 내에서 연결이 없습니다.
  • • 스킵 레이어 연결이 없습니다.
• • 이것은 Deep Boltzmann Machine (DBM)이라고 불립니다.
  • • 연결이 많이없는 일반적인 볼츠만 기계입니다.

A puzzle

• • Why can we estimate the “negative phase statistics” well with only 100 negative examples to characterize the whole space of possible configurations?
  • – For all interesting problems the GLOBAL configuration space is highly multi-modal.
  • – How does it manage to find and represent all the modes with only 100 particles?
• 가능한 구성의 전체 공간을 특성화하기 위해 100 가지의 부정적인 예제만으로 "부정적인 위상 통계"를 추정 할 수있는 이유는 무엇입니까?
  • • 모든 흥미로운 문제에 대해 GLOBAL 구성 공간은 고도의 멀티 모달입니다.
  • • 100 개의 입자만으로 모든 모드를 찾아 내고 표현하는 방법은 무엇입니까?

The learning raises the effective mixing rate.

(학습은 효과적인 혼합 비율을 높입니다.)

• • The learning interacts with the Markov chain that is being used to gather the “negative statistics” (i.e. the data independent statistics).
  • – We cannot analyse the learning by viewing it as an outer loop and the gathering of statistics as an inner loop.
• • Wherever the fantasy particles outnumber the positive data, the energy surface is raised.
  • – This makes the fantasies rush around hyperactively.
  • – They move around MUCH faster than the mixing rate of the Markov chain defined by the static current weights.
• • 학습은 "negative statistics"(즉, 데이터 도립 통계)를 수집하는 데 사용되는 마르코프 체인과 상호 작용합니다.
  • • 학습을 외부 루프로 보고 통계를 내부 루프로 간주하여 학습을 분석 할 수는 없습니다.
• • 판타지 입자가 양의 데이터보다 더 많으면 에너지 표면이 올라갑니다.
  • • 이로 인해 환상이 지나치게 활발하게 진행됩니다.
  • • 정적 현재 무게에 의해 정의 된 마르코프 체인의 혼합 비율보다 훨씬 빠르게 움직입니다.

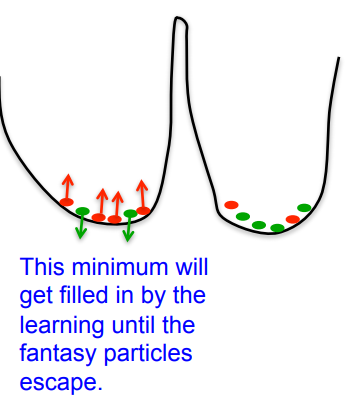
How fantasy particles move between the model’s modes

• • If a mode has more fantasy particles than data, the energy surface is raised until the fantasy particles escape.
  • – This can overcome energy barriers that would be too high for the Markov chain to jump in a reasonable time.
• • The energy surface is being changed to help mixing in addition to defining the model.
• • Once the fantasy particles have filled in a hole, they rush off somewhere else to deal with the next problem.
  • – They are like investigative journalists.