Lecture 11d Using stochastic units to improve search

Noisy networks find better energy minima

• A Hopfield net always makes decisions that reduce the energy.

– This makes it impossible to escape from local minima.

• We can use random noise to escape from poor minima.

– Start with a lot of noise so its easy to cross energy barriers.

– Slowly reduce the noise so that the system ends up in a deep minimum. This is “simulated annealing” (Kirkpatrick et.al. 1981)

• Hopfield net은 항상 에너지를 감소시키는 결정을 내립니다.

• 이로 인해 로컬 미니 마에서 벗어날 수 없습니다.

• 우리는 가난한 최소치로부터 벗어나기 위해 무작위 잡음을 사용할 수 있습니다.

• 에너지 장벽을 넘기 쉽도록 많은 소음으로 시작하십시오.

• 시스템이 최소로 끝나도록 천천히 소음을 줄입니다. 이것은 "시뮬레이트 된 어닐링"(Kirkpatrick et al., 1981)

How temperature affects transition probabilities

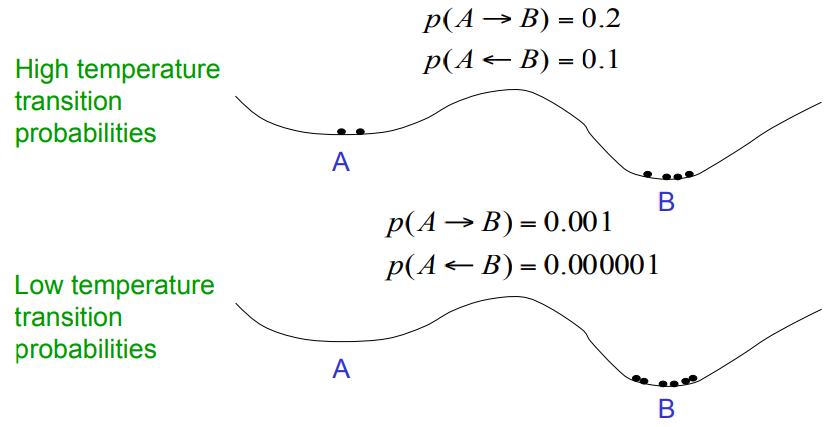
Stochastic binary units

Replace the binary threshold units by binary stochastic units that make biased random decisions.

– The “temperature” controls the amount of noise

– Raising the noise level is equivalent to decreasing all the energy gaps between configurations.

binary threshold units를 바이어스 된 랜덤 결정을 내리는 binary stochastic units로 바꿉니다.

• "온도"는 소음의 양을 조절합니다.

• 잡음 레벨을 높이는 것은 구성 사이의 모든 에너지 차이를 줄이는 것과 같습니다.

Simulated annealing is a distraction

(시뮬레이션 된 어닐링은 산만 함입니다.)

• • Simulated annealing is a powerful method for improving searches that get stuck in local optima.
• • It was one of the ideas that led to Boltzmann machines.

• • But it’s a big distraction from the main ideas behind Boltzmann machines.

  • – So it will not be covered in this course.
  • – From now on, we will use binary stochastic units that have a temperature of 1.

• 시뮬레이트 된 어닐링은 로컬 최적화에서 고착되는 검색을 개선하는 강력한 방법입니다.

• Boltzmann machines로 인도한 아이디어 중 하나였습니다.

• 그러나 그것은 볼츠만 기계의 주요 아이디어에서 큰 혼란을 낳습니다.

  • • 그래서이 과정에서 다루지 않을 것입니다.
  • • 이제부터는 온도가 1 인 이진 확률 적 단위를 사용할 것입니다.

Thermal equilibrium at a temperature of 1

(온도 1에서의 열 평형)

• • Thermal equilibrium is a difficult concept!

  • – Reaching thermal equilibrium does not mean that the system has settled down into the lowest energy configuration.
  • – The thing that settles down is the probability distribution over configurations.
  • – This settles to the stationary distribution.

• • 열 평형은 어려운 개념입니다!

• • • 열 평형에 도달한다고해서 시스템이 최저 에너지 구성으로 정착했다는 의미는 아닙니다.
  • • 안정된 것은 구성에 대한 확률 분포입니다.
  • • 이것은 고정 분포(정상분포)에 놓입니다.

• +) stationary distribution 는 energy function 에 의해 결정됩니다.

• • There is a nice intuitive way to think about thermal equilibrium:

  • – Imagine a huge ensemble of systems that all have exactly the same energy function.
  • – The probability of a configuration is just the fraction of the systems that have that configuration.

• • 열 평형에 대해 생각할 수 있는 좋은 직관적인 방법이 있습니다.

  • • 모두 똑같은 에너지 함수를 가진 거대한 앙상블 시스템을 상상해보십시오.
  • • 구성 확률은 해당 구성을 갖는 시스템의 일부일 뿐입니다.

Approaching thermal equilibrium

• • We start with any distribution we like over all the identical systems.
  • – We could start with all the systems in the same configuration.
  • – Or with an equal number of systems in each possible configuration.
• • Then we keep applying our stochastic update rule to pick the next configuration for each individual system.

• • After running the systems stochastically in the right way, we may eventually reach a situation where the fraction of systems in each configuration remains constant.

  • – This is the stationary distribution that physicists call thermal equilibrium.
  • – Any given system keeps changing its configuration, but the fraction of systems in each configuration does not change.

• • 우리는 모든 동일한 시스템에서 우리가 좋아하는 배포로 시작합니다.

  • • 모든 시스템을 동일한 구성으로 시작할 수 있습니다.
  • • 또는 가능한 모든 구성에서 동일한 수의 시스템을 사용하십시오.
• • 그런 다음 우리는 확률적인 업데이트 규칙을 적용하여 각 개별 시스템에 대한 다음 구성을 선택합니다.
• • 올바른 방식으로 시스템을 확률적으로 실행 한 후에는 각 구성의 시스템 비율이 일정하게 유지되는 상황이 발생할 수 있습니다.
  • • 이것은 물리학자가 열 평형이라고 부르는 고정 분포입니다.
• • 주어진 시스템은 구성을 계속 변경하지만 각 구성의 시스템 비율은 변경되지 않습니다.

An analogy (비유)

• • Imagine a casino in Las Vegas that is full of card dealers (we need many more than 52! of them).
• • We start with all the card packs in standard order and then the dealers all start shuffling their packs.
  • – After a few time steps, the king of spades still has a good chance of being next to the queen of spades. The packs have not yet forgotten where they started.
  • – After prolonged shuffling, the packs will have forgotten where they started. There will be an equal number of packs in each of the 52! possible orders.
• – Once equilibrium has been reached, the number of packs that leave a configuration at each time step will be equal to the number that enter the configuration.

• • The only thing wrong with this analogy is that all the configurations have equal energy, so they all end up with the same probability.

• • 카드 딜러가 가득한 라스베가스의 카지노를 상상해보십시오 (우리는 52 명 이상이 필요합니다).

• • 모든 카드 팩을 표준 주문으로 시작한 다음 딜러가 모두 팩을 뒤섞기 시작합니다.
  • • 스페이드의 왕은 몇 시간 후에 스페이드의 여왕 옆에 있을 가능성이 높습니다. 팩은 그들이 시작한 곳을 아직 잊지 못했습니다.
  • • 장기간의 셔플 후에 팩은 그들이 시작한 곳을 잊어 버릴 것입니다. 각 52 개에 동일한 수의 팩이 있습니다! 가능한 명령.
  • • 일단 평형에 도달하면 각 시간 간격마다 구성을 남기는 팩의 수는 구성에 들어가는 수와 같습니다.
• •이 비유에 잘못된 점은 모든 구성의 에너지가 동일하므로 모두 동일한 확률로 끝난다는 것입니다.