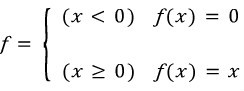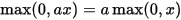http://mongxmongx2.tistory.com/25

ReLu(Rectified Linear Unit)

ReLu는 Rectified Linear Unit의 약자로 해석해보면 정류한 선형 유닛이라고 해석할 수 있다.

Neural Network를 처음배울 때 activation function으로 sigmoid function을 사용한다.

sigmoid function이 연속이여서 미분가능한점과 0과 1사이의 값을 가진다는 점 그리고 0에서 1로 변하는 점이 가파르기 때문에 사용해왔다.

그러나 기존에 사용하던 Simgoid fucntion을 ReLu가 대체하게 된 이유 중 가장 큰 것이 Gradient Vanishing 문제이다.

Gradient Vanishing 이란 말 그대로 Gradient가 사라지는(0으로 수렴하는) 문제이다. 이런 문제가 생기는 이유는 간단하다. Sigmoid 에서 Gradient는 0 ~ 1사이의 값이 나온다. 근데 Backpropagation을 하면서 layer를 거듭하면 거듭할 수록 계속해서 Gradient를 곱하게 되는데 0.xxxx를 계속 곱하다 보니 값이 점점 작아져서 Gradient가 0에 수렴하게 되는 것이다. 그래서 직접 실험을 해보면 hidden layer가 9개, 10개 정도 되면 네트워크가 잘 작동하지 않는다는 것을 알게된다.

따라서 이러한 문제를 해결하기위해 ReLu를 새로운 activation function을 사용한다. ReLu는 입력값이 0보다 작으면 0이고 0보다 크면 입력값 그대로를 내보낸다.

이러한 ReLu가 가지는 이점은 다음과 같다.

1. Sparse activation : 0이하의 입력에 대해 0을 출력함으로 부분적으로 활성화 시킬수 있다.

2. Efficient gradient propagtion : gradient의 vanishing이 없으며 gradient가 exploding 되지 않는다.

3. Efficient computation : 선형함수이므로 미분 계산이 매우 간단하다.

4. Scale-invariant :

하지만 ReLU가 음수들을 모두 0으로 처리하기 때문에 한번 음수가 나오면 더이상 그

노드는 학습되지 않는다는 단점이 한가지 생긴다. 따라서

간단한 네트워크에 대해서는 오히려 좋지 않은 성능을 낼 수도 있다. (물론 이것 때문에 leaky ReLU나 다른 ReLU 함수들이 있기도 하다.)